Divide and Conquer is a programming technique which makes the program more efficient to write. And this technique work on the concept of recursion to solve a problem step by step. Generally this technique work in three parts:- Divide:- Divide the problem into some subproblem. Conquer:- Conquer the subproblem by calling recursively until subproblem solved. Combine:- (Optional Step) Combine the subproblem solution. So, that we will get the final problem Solution. When the subproblems are large enough to solve recursively, we call the recursive case. Once the subproblem becomes small enough that we no longer recursive, we say that the recursion "bottom out" and that we have gotten down to the base case. Application of Divide and Conquer Quick Sort Strassen's algorithm for matrix multiplication Merge Sort Counting inversions Binary Search Finding Min and ...
Divide and Conquer is a programming technique which makes the program more efficient to write.
And this technique work on the concept of recursion to solve a problem step by step.
Generally this technique work in three parts:-
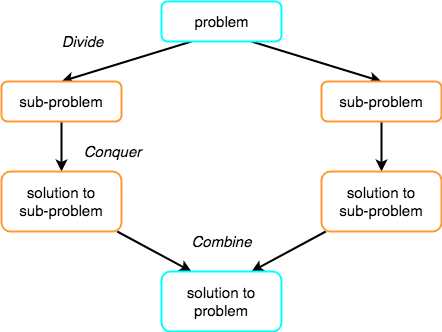
And this technique work on the concept of recursion to solve a problem step by step.
Generally this technique work in three parts:-
- Divide:- Divide the problem into some subproblem.
- Conquer:- Conquer the subproblem by calling recursively until subproblem solved.
- Combine:- (Optional Step) Combine the subproblem solution. So, that we will get the final problem Solution.

Application of Divide and Conquer
- Quick Sort
- Strassen's algorithm for matrix multiplication
- Merge Sort
- Counting inversions
- Binary Search
- Finding Min and max
Divide and Conquer Abstract Algorithm
DAC(a,i,j)
{
//small(a,i,j) represent the smallest subproblem which can't be further divided
if(small(a,i,j))
//solution(a,i,j) return some constant value
return(solution(a,i,j));
else
{
//Divide(a,i,j) represent the dividing of large problem into small
mid=Divide(a,i,j);
b=DAC(a,i,mid);
c=DAC(a,mid+1,j);
//combine(b,c) represnt merging up of small subproblem
d=combine(b,c);
return d;
}
}
About Complexity of Abstract Divide & Conquer Algorithm
small(a,i,j) having O(1) time complexity
solution(a,i,j) having O(1) time complexity
Divide(a,i,j) having some constant C1 time complexity
b=DAC(a,i,mid); having T(n/2) time complexity
c=DAC(a,i,mid); also having T(n/2) time complexity
combine(b,c) having some constant C2 time complexity
The total time complexity of Divide and Conquer
T(n)=O(1) if n is small
T(n)=C1+T(n/2)+T(n/2)+C2 if n is large
assuming C=C1+C2
Then,
T(n)=2T(n/2)+C //for two equal subproblem cost
And for 'a' equal subproblem of size 'b'
T(n)=aT(n/b)+C //It also depict that Divide and Conquer can be solved by Master's Theorem
Important Points about Divide & Conquer
- Function calling occur in Preorder
- Execution of function happen in Postorder
good explained
ReplyDelete